Problems

• Decaying learning rates provide googd compromise between escaping poor local minima and convergence
• Many of the convergence issues arise because we force the same learning rate on all parameters
• Try to releasing the requirement that a fixed step size is used across all dimensions
• To be clear, backpropagation is a way to compute derivative, not a algorithm
  • The below is NOT grident desent algorithm

Better convergence strategy

Derivative-inspired algorithms

RProp

• Resilient propagation
• Simple first-order algorithm, to be followed independently for each component
  • Steps in different directions are not coupled
• At each time
  • If the derivative at the current location recommends continuing in the same direction as before (i.e. has not changed sign from earlier):
    • Increase the step($\alpha$ > 1), and continue in the same direction
  • If the derivative has changed sign (i.e. we’ve overshot a minimum)
    • Reduce the step($\beta < 1$) and reverse direction

• Features
  • It is frequently much more efficient than gradient descent
  • No convexity assumption

QuickProp

• Newton updates

$\mathbf{w}^{(k+1)}=\mathbf{w}^{(k)}-\eta \mathbf{A}^{-1} \nabla_{\mathbf{w}} E\left(\mathbf{w}^{(k)}\right)^{T}$

• Quickprop employs the Newton updates with two modifications

• It treats each dimension independently

$w_{i}^{k+1}=w_{i}^{k}-E^{\prime \prime}\left(w_{i}^{k} | w_{j}^{k}, j \neq i\right)^{-1} E^{\prime}\left(w_{i}^{k} | w_{j}^{k}, j \neq i\right)$

• It approximates the second derivative through finite differences

$w_{l, i j}^{(k+1)}=w_{l, i j}^{(k)}-\frac{\Delta w_{l, i j}^{(k-1)}}{E r r^{\prime}\left(w_{l, i j}^{(k)}\right)-E r r^{\prime}\left(w_{l, i j}^{(k-1)}\right)} \operatorname{Err}^{\prime}\left(w_{l, i j}^{(k)}\right)$

• Features
  • Employs Newton updates with empirically derived derivatives
  • Prone to some instability for non-convex objective functions
  • But is still one of the fastest training algorithms for many problems

Momentum methods

• Insight
  • In the direction that converges, it keeps pointing in the same direction
    • Need keep track of oscillations
    • Emphasize steps in directions that converge smoothly
  • In the direction that overshoots, it steps back and forth
    • Shrink steps in directions that bounce around
• Maintain a running average of all past steps
  • Get longer in directions where gradient stays in the same sign
  • Become shorter in directions where the sign keep flipping
• Update with the running average, rather than the current gradient
  • Emphasize directions of steady improvement are demonstrably superior to other methods
• Momentum Update

$\Delta W^{(k)}=\beta \Delta W^{(k-1)}-\eta \nabla_{W} \operatorname{Loss}\left(W^{(k-1)}\right)^{T}$

${W^{(k)}=W^{(k-1)}+\Delta W^{(k)}}$

• First computes the gradient step at the current location: $-\eta \nabla_{W} \operatorname{Loss}\left(W^{(k-1)}\right)^{T}$
• Then adds in the scaled previous step: $\beta \Delta W^{(k-1)}$

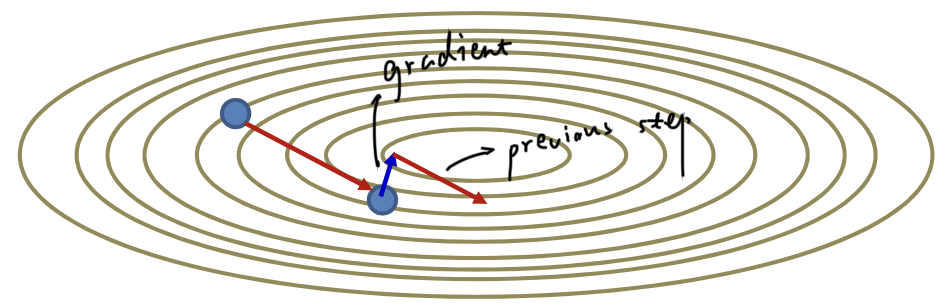
Nestorov’s Accelerated Gradient

• Change the order of operations

$\Delta W^{(k)}=\beta \Delta W^{(k-1)}-\eta \nabla_{W} \operatorname{Loss}\left(W^{(k-1)}+\beta \Delta W^{(k-1)}\right)^{T}$

${W^{(k)}=W^{(k-1)}+\Delta W^{(k)}}$

• First extend the previous step: $\beta \Delta W^{(k-1)}$
• Then compute the gradient step at the resultant position: $-\eta \nabla_{W} \operatorname{Loss}\left(W^{(k-1)}+\beta \Delta W^{(k-1)}\right)^{T}$
• Add the two to obtain the final step
• Converges much faster than momentum

Summary

• Try the step size for all dimension is bad
  • Treat each dimension independently
• Try to normalize curvature in all directions
  • Second order methods, e.g. Newton's method
  • Too expensive: require inversion of a giant Hessian
• Treat each dimension independently
  • RProp / QucikProp
  • Works, but ignores dependence between dimensions
  • Can still be too slow
• Momentum methods which emphasize directions of steady improvement are demonstrably superior to other methods

Incremental updates

• Batch gradient descent
  • Try to simultaneously adjust the function at all training points
  • We must process all training points before making a single adjustment
• Stochastic gradient descent
  • Adjust the function at one training point at a time
  • A single pass through the entire training data is called an “epoch”
    • An epoch over a training set with $T$ samples result in $T$ updates of parameters
  • We must go through them randomly to get more convergent behavior
    • Otherwise we may get cyclic behavior (hard to converge)
  • Learning rate
    • Correcting the function for individual instances will lead to never-ending, non-convergent updates (correct one, and miss the other)
    • The learning will continuously “chase” the latest sample
    • Correction for individual instances with the eventual miniscule learning rates will not modify the function

• Drewbacks

  • Batch / Stochastic gradient descent is an unbiased estimate of the expected loss

  $E[\operatorname{Loss}(f(X ; W), g(X))]=E[\operatorname{div}(f(X ; W), g(X))]$

  • But the variance of the empirical risk in batch gradient is {% math_inline %}\frac{1}{N}{% endmath_inline %} times compared to stochastic gradient descent
  • Like using {% math_inline %}\frac{1}{N}\sum{X}{% endmath_inline %} and {% math_inline %}X_i{% endmath_inline %} to estimate {% math_inline %}\bar{X}{% endmath_inline %}

• Mini-batch gradient descent

  • Adjust the function at a small, randomly chosen subset of points
  • Also an unbiased estimate of the expected error, and the variance is relatively small compared to SGD
  • The mini-batch size is a hyper parameter to be optimized
  • Convergence depends on learning rate
    • Simple technique: fix learning rate until the error plateaus, then reduce learning rate by a fixed factor (e.g. 10)
    • Advanced methods: Adaptive updates, where the learning rate is itself determined as part of the estimation